1525. Задача группирования

Имеется множество из n целых чисел. Из любых k разных элементов Вы можете составить группу. Две группы считаются разными, если у них имеется хотя бы один не общий элемент. Например, если имеются 4 элемента a, b, c, d и Вам необходимо составить группы из двух элементов, то возможными допустимыми группами будут ab, ad, bc, cd. Систему групп будем называть полной для заданного k, если количество групп в ней максимально возможное. Например, для предыдущего примера {ab, bc, cd, bd, ad, ac} является полной системой групп.

Удобство полной системы групп будем вычислять следующим образом:

1. Каждая группа делает свой вклад в систему – произведение чисел в группе;

2. Вклады всех групп складываются;

3. Удобство системы эквивалентно общему вкладу mod m, где m – ограничивающий параметр.

В нашем примере для k = 2 удобство равно F₂ = (ab + bc + cd + bd + ad + ac) mod m. При k = 1 удобство равно F₁ = (a + b + c + d) mod m.

Вам следует найти полную систему групп с максимальным удобством.

Вход. Каждый тест начинается двумя натуральными числами n (2 ≤ n ≤ 1000) и m (1 ≤ m < 2³¹). Следующая строка содержит n натуральных чисел, каждое из которых не больше 1000. Последний тест содержит n = m = 0 и не обрабатывается.

Выход. Для каждого теста в отдельной строке вывести максимальное значение удобства среди всех полных систем групп.

Пример входа	Пример выхода
4 10 1 2 3 4 4 100 1 2 3 4 4 6 1 2 3 4 0 0	5 50 5

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Пусть а₁, a₂, …, a_n – заданные n чисел. Обозначим через F_ik (i ³ k) сумму всех возможных произведений по k чисел, взятых среди первых i чисел a₁, …, a_i. Построим следующую таблицу F_ik:

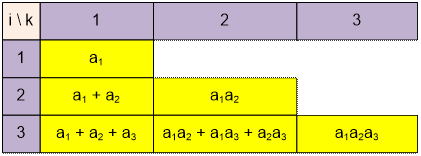
Для четырех чисел соответственно получим:

· F_4,1 = a₁ + a₂ + a₃ + a₄;

· F_4,2 = a₁a₂ + a₁a₃ + a₁a₄ + a₂a₃ + a₂a₄ + a₃a₄;

· F_4,3 = a₁a₂a₃ + a₁a₂a₄ + a₁a₃a₄ + a₂a₃a₄;

· F_4,4 = a₁a₂a₃a₄;

Имеют место следующие рекуррентные соотношения:

F_i1 = F_(i-1)1 + a_i, F_ii = F_{(i-1) (i-1)} * a_i, 1 £ i £ n

F_ik = F_(i-1)k + F_{(i-1) (k-1)} * a_i, 1 £ i £ n, 1 < k < i

Например,

· F_3,2 = F_2,2 + F_2,1 * a₃ = a₁a₂ + (a₁ + a₂) * a₃ = a₁a₂ + a₁a₃ + a₂a₃;

· F_4,3 = F_3,3 + F_3,2 * a₄ = a₁a₂a₃ + (a₁a₂ + a₁a₃ + a₂a₃) * a₄ =

a₁a₂a₃ + a₁a₂a₄ + a₁a₃a₄ + a₂a₃a₄

Значения каждой следующей строки пересчитываются через значения предыдущей строки, поэтому в памяти достаточно хранить один линейный массив d размера 1000. При этом пересчет значений i - ой строки следует начинать с конца: сначала вычислить F_ii, потом F_i(i-1) и так далее до F_i1. Все вычисления следует проводить по модулю m.

Пример

Рассмотрим первый тест. Построим две таблицы: вычисления во второй будут производиться по модулю m = 10, а в первой – нет.

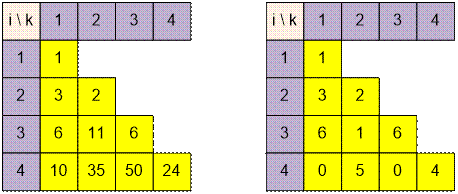
Например,

· F_4,2 = F_3,2 + F_3,1 * 4 = 11 + 6 * 4 = 35;

· F_4,3 = F_3,3 + F_3,2 * 4 = 6 + 11 * 4 = 50;

Ответом является максимальное число в четвертой строке второй таблицы.

Реализация алгоритма

Объявим линейный массив d, в котором будут пересчитываться значения F_ik.

long long d[1000];

Вводим количество чисел n и значение m. Для каждого входного теста изначально обнуляем массив d. Первое число a₁ заносим в d[0].

while(scanf("%lld %lld",&n,&m), n + m > 0)

{

memset(d,0,sizeof(d));

scanf("%lld",&d[0]);

Вводим значение x = a_i+1 (1 £ i < n) и пересчитываем значения F_ik, k = i, i – 1, …, 1 по выше приведенным рекуррентным формулам. Все вычисления проводим по модулю m.

for(i = 1; i < n; i++)

{

scanf("%lld",&x);

d[i] = (d[i-1] * x) % m;

for(j = i - 1; j > 0; j--)

d[j] = (d[j-1] * x + d[j]) % m;

d[0] = (d[0] + x) % m;

}

Находим максимальное значение среди элементов массива d и заносим его в переменную res.

res = 0;

for(i = 0; i < n; i++)

if (d[i] > res) res = d[i];

Выводим результат.

printf("%lld\n",res);

}